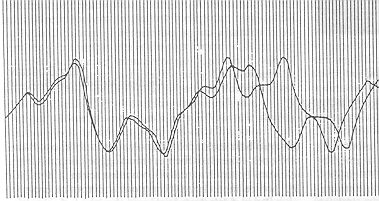
1. ábra Az időjárás két, közel azonos kezdőfeltételből számított folyamatának szétválása a múló időben, Lorenz 1961-ben végzett vizsgálatai szerint.
dátum: 2009.4.20. fájl: html-2009/kaosz-02.htm C. 09961-68
Fizikai Szemle 1993/12. 487.o.
Götz Gusztáv
Országos Meteorológiai Szolgálat
Harminc esztendővel ezelőtt, 1963-ban jelent meg Edward N. Lorenz tanulmánya, amelyben az amerikai Massachusetts Institute of Technology (MIT) elméleti meteorológus professzora kimutatta, hogy determinisztikus rendszerek is tanúsíthatnak előre nem látható, véletlenszerű viselkedést. Ennek a különös viselkedési formának egy évtizeddel később James A. Yorke amerikai matematikus a kissé megtévesztő káosz nevet adta. A káosz felfedezése alapvetően megváltoztatta a világról alkotott képet, és ezért azt sokan, Einstein relativitáselmélete és Heisenberg kvantummechanikája mellé sorolva, a 20. század harmadik forradalmasító tudományos vívmányának tekintik. "A relativitáselmélet megsemmisítette az abszolút tér és idő létezéséről kialakított newtoni illúziót; a kvantumelmélet megsemmisítette Newton álmát egy ellenőrizhető mérési eljárásról; a káosz pedig megsemmisíti a determinisztikus előrejelezhetőség laplace-i látomását" - mondta egy fizikus. Hogyan jutott egy meteorológus ilyen jelentőségű felismerésre? Erről szólnak az alábbi sorok.
A pillangó-hatás
A Heisenberg-féle határozatlansági reláción felnevelkedett, modern természetkutató szemében talán már a bohózat világába tartozik a két évszázaddal korábban munkálkodó francia filozófus-matematikus Laplace márki optimizmusa, aki hitt egy szuper-intelligencia létezésében, amely ugyanabba a formulába képes összesűríteni az Univerzum legnagyobb képződményei és a legkisebb atom mozgásait; számára semmi nem bizonytalan, és a jövő, csakúgy mint a múlt, ott lebeg a szeme előtt. Századunkban már óvatosabban illett a tudomány filozofikus magvát megfogalmazni: ha adottak egy rendszer kezdőfeltételeiről a közelítő ismeretek, akkor a természeti törvények birtokában kiszámítható a rendszer közelítő viselkedése. Az egyik oktató előszeretettel ismételte el hallgatóinak: "A Nyugat tudományának alapelve, hogy nem kell számításba vennünk egy másik galaxis valamelyik bolygóján a lehulló falevelet, ha a Földünkön álló asztalon egy biliárdgolyó mozgását kívánjuk meghatározni. Az igen kis hatások elhanyagolhatóak. Van a dolgok működésében valamiféle konvergencia, ezért tetszőlegesen kicsiny hatások nem robbannak fel, és nem járnak tetszőlegesen nagy következményekkel."
A közelítésbe és a konvergenciába vetett hitet a klasszikus tények igazolták - a filozófia működött. A Halley-üstökös 1910-es helyzetének azonosításánál elkövetett apró hiba csak apró hibát okozott az 1986-os visszatérésének előrejelzésében. A számítógépek is erre a feltételezésre építenek az űrhajó irányítása során: a közelítőleg pontos input közelítőleg pontos output-ot eredményez. Erre a feltételezésre alapoznak a gazdasági szakértők is, noha prognózisaik sikere kevésbé szembeötlő. És ugyanezen a feltételezésen nyugodtak a numerikus időjárás előrejelzés úttörőinek munkái is.
Edward N. Lorenz fölfedezése - a pillangó-hatás - a tudósok e hitbe vetett bizalmát alapjaiban rendítette meg. Lorenz kezdetben egy sirály metaforáját használta; az előbbi, maradandóbbá vált festői elnevezés valószínűleg a tudomány előmozdítására alakult amerikai asszociáció (AAAS) Washingtonban, 1979. december 29-én tartott éves ülésén elmondott előadásából ered. A beszéd címe ugyanis a következőképpen hangzott: "Előrejelezhetőség: képes-e egy pillangó brazíliai szárnycsapása Texasban tornádót kiváltani?". És a szerző előadásának végén erre a kérdésre igenlő elvi választ adott.
Ki ez a tudós, és milyen gondolatok vezették egyre közelebb e bizarr következtetéshez?
Aki felfedezte a káoszt
Barátai és ismerősei szerint Edward N. Lorenz különös vágású meteorológus. Gyűrött arca egy jenki farmer képéhez hasonlatos, meglepően csillogó szemeivel úgy tűnik, mintha állandóan nevetne. Magáról vagy a munkájáról ritkán beszél, de szeret másokat hallgatni. Gyakran merül el számításainak és álmainak világába, és ilyenkor megközelíthetetlenné válik munkatársai számára. Legközelebbi barátai úgy vélik, Lorenz az idejének jelentős részét tölti el valamiféle távoli, külső térben.
Fiatal korában az időjárás lelkes megfigyelője volt, legalábbis olyan mértékben, hogy kitartóan vezette a szülei Connecticut állambeli West Hartford-i házának kertjében elhelyezett max-min hőmérő leolvasásait. De ennél is több időt szentelt a házon belül különböző matematikai feladványok megoldásának. Olykor édesapjával együtt törték a fejüket egy-egy rejtvény megfejtésén. Egyszer egy különösen bonyolult probléma került eléjük, amelyről kiderült, hogy nincs megoldása. Ez teljesen elfogadható - mondta az atya -, mindig próbálkozhatunk egy kérdést úgy megoldani, hogy bebizonyítjuk: a megoldás nem létezik. Az ifjúnak tetszett az ötlet, hiszen mindig is szerette a matematika tisztaságát, és amikor 1938-ban a Dartmouth College-ban elvégezte tanulmányait, úgy gondolta, hogy az elméleti matematika iránt érez elhívatást.

1. ábra Az időjárás két, közel azonos kezdőfeltételből számított folyamatának szétválása a múló időben, Lorenz 1961-ben végzett vizsgálatai szerint.
A történelmi események azonban közbeszóltak: az Egyesült Államoknak a II. Világháborúba történt belépésével a matematikus-jelöltet azon nyomban besorozták egy időjárás előrejelzők számára az MIT-ben rendezett speciális oktatási kurzus hallgatói közé, majd Lorenz a U.S. Army Air Corps előrejelző tisztje lett. A meteorológiával a háborús évek során kötött barátsága elszakíthatatlannak bizonyult; Lorenz elhatározta, hogy életét a légköri folyamatok elméleti vizsgálatának szenteli.
Az elektronikus számítógépekre alapozott numerikus időjárás prognosztika kibontakozásának leglelkesebb időszakában nyilvánvalóan nagy feltűnést keltett az a statisztikus meteorológusok körében elterjedő nézet, amely feltételezhetően Norbert Wiener egyik 1956-ban tartott előadásának hibás értelmezéséből fakadt. E nézet szerint ugyanis azoknak az alkalmasan megválasztott lineáris előrejelzési egyenleteknek, amelyekben a prognosztizált jövőbeli értékek a jelen és a múlt értékek lineáris kombinációiként állnak elő, éppolyan jól kell működniök, mint bármely más elérhető formulának. Lorenz ezt az elgondolást valószínűtlennek tartotta, és gyanúja igazolásához 1960-ban elhatározta egy nemlineáris egyenletrendszer numerikus megoldását oly módon, hogy az output-ot megfigyelési adatoknak tekinti, amelyekre azután alkalmazhatók lesznek az optimális lineáris előrejelzési formulák meghatározásának standard módszerei. Maga az egyenletrendszer a légkör általános cirkulációjának 13 változóra redukált, alacsonyrendű modellje volt, igazodva az MIT-beli irodájában használt kis számítógép kapacitásához. A kísérlet egyértelműen megmutatta a lineáris előrejelzés korlátait.
Lorenz modellje az időjárás különös képét tárja elénk: a Nap olyan égbolton át tűz, amelyen soha nem jelennek meg felhők; a szelek tükörsima felszín fölött fújnak; soha nem száll le az est; az ősz soha nem adja át helyét a télnek; eső soha nem hullik. E furcsa légkör folyamatait szimuláló Royal McBee számítógép - kábelek és elektroncsövek erdeje, amely az iroda nagy részét elfoglalja irritálóan hangos, és hetenként egyszer biztosan elromlik. De ha működik, másodpercenként 60 szorzást végez el, és percenként nyomtatja ki egy újabb nap adatait. Digitalizált ciklonok futják körbe az idealizált féltekét, a nyugati szelek övében hol a zonális áramlás, hol a blocking-helyzet veszi át az uralmat.
Ahogy a kísérletnek híre száll, oktatók és hallgatók állják körül a gépet, fogadásokat kötve: mit fog Lorenz időjárása legközelebb cselekedni. A rendkívül leegyszerűsített modell ugyanis reprodukálni képes a valóságos légkör egyik legalapvetőbb belső tulajdonságát, az aperiodikus viselkedést: soha nem fordul elő kétszer pontosan ugyanaz az eseménysor.
Ezzel megszületik Lorenz első jelentős felismerése: az időjárás aperiodikus változékonyságának kialakulásához nem szükséges, hogy a légkörre ható külső kényszerek aperiodikusan változzanak, sőt még az sem, hogy ezek a kényszerek egyáltalán megváltozzanak.
És megjelenik a káosz...
1961 telének egyik napján Lorenz, miután úgy döntött, hogy az egyik időjárási eseménysort részletesebben is analizálja, leállította a gépet. És ahelyett, hogy az egész addigi futást megismételte volna, a már lezajlott folyamatnak valahová a közepe tájékára ugrott vissza. Kezdeti feltételként a korábban kinyomtatott, erre az időpontra adódott számokat táplálta be, majd, hogy a zajtól megszabaduljon, lesétált a hallba egy csésze kávéra. Egy óra múlva szobájába visszatérve, teljesen váratlan kép tárult a szeme elé: valami, ami egy új tudománynak vetette el a magvát. '
Az új futásnak illett volna pontosan megismételnie a korábbi folyamatot. Hiszen Lorenz saját kezűleg adta be a gépnek a számokat. A program nem változott. Mégis, ahogy a kinyomtatott új eredményekre meredt, azt kellett látnia, hogy ez az időjárási eseménysor olyan gyorsan kezdett távolodni a korábbi számítás során kapottól, hogy néhány hónap múltán a kettő között minden hasonlóság eltűnt: mintha valaki találomra húzott volna ki két időjárási helyzetet egy kalapból. Lorenz első gondolata az volt, hogy ismét valamelyik elektroncső mondta fel a szolgálatot.
De csakhamar fény derült az igazságra. Nem géphibáról volt szó. A probléma a kezdeti feltétel megadásában rejlett. A számítógép memóriája a számokat hat tizedesjegyig tárolta: ,506127 - ám, helykímélés végett, a kinyomtatás csak három tizedesjegyig történt: ,506. Lorenz az új futáshoz kezdőfeltételként ezt a rövidebb, kerekített számot adta meg, úgy vélekedve, hogy a különbség teljesen elhanyagolható.
A következményt az 1. ábrán szemlélhetjük meg. Kezdetben a két időjárási eseménysor szinte tökéletesen együtt halad. A harmadik nagy hullám során azonban megtörténik a szétválás, és a két folyamat között megszűnik minden azonosság.
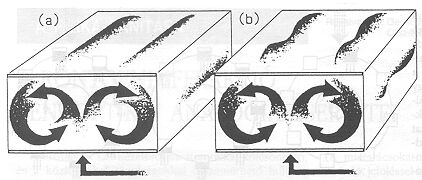
2. ábra A Rayleigh-Bénard-féle cellás konvekció térbeli elrendeződése a vertikális hőmérséklet-különbség két különböző értéke esetén.
Lorenz matematikai intuíciójára vall - amit kollégái csak később kezdtek megérteni -, hogy úgy érezte: a különös eredmény mélyén valami lényeges tulajdonság rejtőzik. Noha a modell csak "nagy paródiája" volt a földi légkörnek, egyszerűségében is tükrözte a valóság egyik alapvető ismérvét: bármelyik fizikai rendszer, amelyik aperiodikusan viselkedik, annak a folyamatai előrejelezhetetlenek. Később kiderült, hogy az aperiodikus viselkedés megjelenése elkerülhetetlen minden általános (legalább két szabadsági fokú), nemlineáris mechanikai rendszerben. Az előrejelezhetetlenség oka az ezekben a rendszerekben törvényszerűen jelentkező pillangó-hatás, illetve, tudományosabb megfogalmazásban, a kezdőfeltételekre mutatott érzékenység, amit dinamikai instabilitásnak is szoktak nevezni. A dinamikai instabilitás révén a megadott kezdőfeltételekben óhatatlanul rejlő kis hibák az idő múlásával a rendszerre jellemző exponenciális mértékben növekednek, és ezért előbb-utóbb a prognózis elveszíti minden gyakorlati értékét. A determinisztikus rendszer viselkedése tehát a kezdeti feltételek rögzítésének időpillanatából szemlélve válik a számunkra, ahogyan a bevezetésben fogalmaztunk, "véletlenszerűvé". A precíz előrejelzés elméletileg természetesen megvalósítható lenne, ha a rendszer állapotának induló értékeit végtelen pontossággal tudnánk megadni.
A véletlenszerű viselkedést mutató determinisztikus rendszerek azután a kaotikus rendszer elnevezést kapták, és a hetvenes évek közepétől a káosz egyre inkább az egyik legaktívabban kutatott téma lett.
Rend a káoszban: a különös attraktor
Lorenz felfedezése tehát, mint láttuk, a szerencsén múlt. Ha akkor megállt volna a pillangó-hatás feltárásánál, amely az előrejelezhetőségnek elvi korlátot szab; és nyomába plántálja a tiszta véletlent, munkája nem jelentett volna többet, mint egy nagyon rossz hírt: a bizonytalanság bizonyosságát: Lorenz azonban többet látott a determinisztikus modelljébe ágyazódott véletlenszerűségnél; megsejtette, hogy a kaotikus viselkedés mögött valamilyen rend is rejtőzik.
E sejtés igazolásához még tovább kellett egyszerűsítenie a vizsgálatra kiszemelt rendszer kormányzó egyenleteit. Végül egy nemlineáris harmadrendű modellnél kötött ki, amely a klasszikus Rayleigh-Bénard féle konvekciót volt hivatott a létező legegyszerűbb formában szimulálni. Ez a mozgásforma két vízszintesen elhelyezett hővezető lemez közötti közeg áramlását jelenti, amely akkor alakul ki, ha az alsó lemezt fűteni kezdjük, és a két lemez közötti hőmérséklet-különbség egy kritikus értéket meghalad. Az áramlási kép kezdetben egymással szemben forgó hengerek sorozatára emlékeztet (2. a ábra), a hőmérséklet-különbség további növelésével azonban a mozgás bonyolultabbá válik: a forgás sebessége ingadozni kezd, és ez az ingadozás előre-hátra mozog a hengerek tengelye mentén (2. b ábra). Mindkét esetben azt várnánk - hiszen ezt tanította a fizika -, hogy idővel a kép állandósul, még az ingadozások is szabályos időközönként ismétlődnek. Lorenz numerikus kísérlete azonban nem ezt mutatta!
A Lorenz-modell három állapotváltozót tartalmazott: a konvektív mozgás intenzitását, a fel- és leáramlások közötti hőmérséklet-különbséget, valamint a közegben kialakuló függőleges hőmérséklet-eloszlás jellemzőjét. Az állapotváltozás ábrázolására Lorenz két módszert választott. Először a megszokott úton felrajzolta egy-egy állapotváltozó időbeli alakulását (3.a ábra). A másodiknál a három állapotváltozó alkotja a koordinátarendszert; ebben a háromdimenziós fázistérben egy pont jelenti a rendszer pillanatnyi állapotát, ezeknek az állapotpontoknak a sorozata (illetve az azokat összekötő trajektória) pedig a rendszer viselkedését ábrázolja. A konvekciós modell kezdeti állapotváltozására a 3.b ábrán, az úgynevezett állandósult viselkedésére pedig a 3.c ábrán szereplő kép adódott.
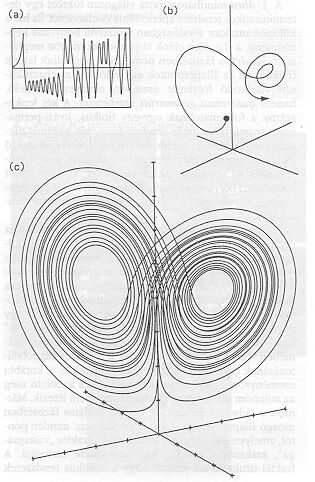
3. ábra A cellás konvekció kaotikus időbeli viselkedése. (a) E=Egy állapotváltozó időbeli menete. (b) A kezdeti, úgynevezett tranziens szakasz a fázistérben. (c) Az állandósult viselkedés a fázistérben: a Lorenz-féle különös attraktor.
Az eredmény a természettudományos közösségre a megdöbbenés erejével hatott. Eddig a fizikusok a korlátos energiájú determinisztikus rendszerek állandósult viselkedésének három típusát ismerték; ezek fázistérbeli geometriai alakzatát (úgynevezett attraktorát) a nyugalmi állapotot képviselő pont, a periodikus változást ábrázoló zárt görbe, kvázi-periodikus folyamatok esetében pedig egy tórusz jelenti. Most viszont feltűnt egy negyedik típus is, a 3.c ábrán látható különös attraktor, amely jellegzetes lepkeszárny vagy bagolyszem alakjával később a káosz emblémája lett.
A 3. ábra mindhárom rajza világosan tükrözi egy determinisztikus rendszer aperiodikus viselkedését. És bár a különös attraktor a valóságban rendkívül bonyolult képződmény, a 3.c ábra elénk tárja a káosz mögött meghúzódó rendet: a fázistérben nem elkent pontfelhőt látunk (miként ott az állapotpontok egy valóban sztochasztikusan viselkedő folyamat esetében elhelyezkednének), hanem határozott geometriai szerkezetet. A két lepkeszárny a folyamatoknak egy-egy tipikus, kvázi-permanens áramlási rezsimbe rendeződésre való hajlamát tükrözi, a légkör általános cirkulációja esetében például a fő makroszinoptikus helyzetek kialakulását. A prognosztizőri székből szemlélve az eseményeket, az állapotpont kaotikusan bolyong az egyik lepkeszárnyon, és véletlenszerűen következik be a váltás, a másik szárnyra (rezsimbe) történő átugrása is.
A Lorenz-féle különös attraktor említett bonyolultsága olyan téma, amelyről ma már könyveket írnak. Gondoljunk bele: a rendszer állandósult állapotváltozása egyrészt a végtelen felé haladó időben, másrészt egy korlátos kiterjedésű fázistérben bonyolódik le, ám eközben a mozgó állapotpont soha nem érintheti újból az általa kirajzolt trajektória egyetlen pontját sem! Ha ugyanis egy ilyen, valamelyik múltbeli állapottal történő "találkozás" bekövetkeznék, akkor - a dinamika alaptörvénye értelmében - ettől a pillanattól kezdve a rendszer állapotváltozásának pontosan meg kellene ismételnie a korábbi eseménysort. Ilyen periodikus viselkedés azonban még az autonóm nemlineáris rendszerekben sem létezik. Mármost a "lehetőségét" annak, hogy a korlátos fázistérben mozgó állapotpont valóban "elkerülhessen" minden pontot, amelyen előzőleg már áthaladt, az attraktor "vastagsága", szakszóval annak fraktál-szerkezete biztosítja. A fraktál-struktúra azt jelenti, hogy a kaotikus rendszerek
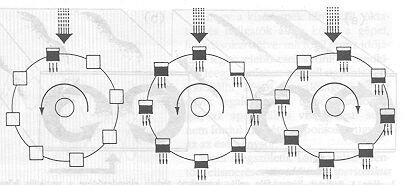
4. ábra A kaotikus forgású Lorenz-féle vízikerék.
különös attraktorai nem sima topológiai sokaságok, hanem speciális képződmények: olyan alakzatok, amelyeknek a dimenziója nem fejezhető ki egész számmal, és amelyek annál több részletet mutatnak, minél jobban felnagyítjuk őket. A 3. c ábra háromdimenziós fázisterébe ágyazott attraktor kétdimenziós rajza valójában 2,06-dimenziós formáció.
Kezdetben Lorenz kísérletéről kevesen tudtak. Amikor Willem Malkus, az MIT alkalmazott matematika professzora először értesült róla, nevetve mondta: "Ugyan Ed, tudjuk, nagyon jól tudjuk, hogy a folyadék-konvekció egyáltalában nem így viselkedik". A komplexitás később biztosan eltűnik, folytatta, és a rendszer stacionárius, szabályos mozgásban állapodik meg.
Ma ott áll Malkus alagsori laboratóriumában az általa szerkesztett Lorenz-féle vízikerék, hogy ő maga demonstrálja a hitetlenkedőknek a káosz mechanikai analógját. Egy kerék peremén kis edények függenek (4. ábra), amelyekbe felülről víz csorog. Az edényekből a víz a talpukon lévő kis lyukon folyik ki. Ha a vízutánpótlás elég gyors, a kerék állandó forgásba lendül. Ha pedig még gyorsabb, akkor vízzel telt edények is emelkednek, súlyuk lelassítja, majd megállítja és ellenkező irányú forgásba hozza a kereket. A forgás iránya és sebessége ezt követően, a beépített nemlineáris hatás révén, teljesen véletlenszerűvé, kaotikussá válik.
Egy nemlineáris dinamika hajnala
A káosz felfedezése nyomán új tudományág született, a nemlineáris dinamika. Művelői még csak az első tapogatódzó lépéseknél tartanak, de máris egy új világkép tárul eléjük. Matematikusok, fizikusok, csillagászok, biológusok, a közgazdaságtan és az orvostudományok szakértői elemzik területük nemlineáris rendszereinek viselkedését. És - tapasztalva a "determinisztikus véletlenek" sorozatát - néha újból felfedezik maguknak a káoszt.
Lorenz 30 évvel ezelőtt írta meg "Deterministic nonperiodic flow" című tanulmányát, amelyben a cellás konvekció egyszerű modelljével nyert eredményeiről beszámolt. A dolgozat fizikus körökben közel tíz éven át ismeretlen maradt. Hiszen Lorenz meteorológus volt, és kinek jutott volna eszébe, hogy a káoszt a Journal of the Atmospheric Sciences 20. kötetének 130. oldalán keresse.